EE274 (Fall 23): Homework-2

Focus area: Lossless Compression
Due Date: Nov 1, midnight (11:59 PM)
Weightage: 15%
Total Points: 110
Submission Instructions: Provided at the end of HW (ensure you read these!)
Submission link:
- For written part: HW2-Written
- For programming part: HW2-Code

Please ensure that you follow the Stanford Honor Code while doing the homework. You are encouraged to discuss the homework with your classmates, but you should write your own solutions and code. You are also encouraged to use the internet to look up the syntax of the programming language, but you should not copy-paste code from the internet. If you are unsure about what is allowed, please ask the instructors.

Note for the coding part
Before starting the coding related HW1 questions ensure following instructions from HW1 are followed:

Ensure you are using the latest version of the SCL EE274/HWs GitHub branch. To ensure run the following command in the SCL repository you cloned from HW1:
```
git status
```
You should get an output saying On branch EE274_Fall23/HWs. If not, run the following command to switch to the correct branch:
```
git checkout EE274_Fall23/HWs
```
Finally ensure you are on the latest commit by running:
```
git pull
```
You should see a HW2 folder in the HWs folder.
Ensure you are in the right conda environment you created in HW1. To ensure run the following command:
```
conda activate ee274_env
```
Before starting, ensure the previous tests are passing as expected. To do so, run following from stanford_compression_library folder:
```
find scl -name "*.py" -exec py.test -s -v {} +
```
and ensure tests except in HW folders pass.

Q1: Camping Trip (20 points)

During one of the camping trips, Pulkit was given $n$ rope segments of lengths $l_{1}, l_{2}, \dots, l_{n}$ by Kedar, and was asked to join all the ropes into a single long segment of length $\sum_{i = 1}^{n} l_{i}$ . Pulkit can only join two ropes at a time and the "effort" in joining ropes $i, j$ using a knot is $l_{i} + l_{j}$ . Pulkit is lazy and would like to minimize his "effort" to join all the segments together.

[5 points] Do you see any parallels between the problem and one of the prefix-free codes you have learnt about? Please justify your answer.
[5 points] Let $E_{o pt}$ be the optimal (minimal) value for the effort required to join all the segments. Without solving the problem, can Pulkit get an estimate of what the $E_{o pt}$ would be? Leaving your answer in terms of inequalities is fine.
[10 points] Implement the function compute_minimum_effort() in the file hw2_p1.py.
HINT: You may use one of the prefix-free code implementations in the SCL Library

Q2: Generating random non-uniform data (25 points)

Consider the problem of sampling a non-uniform discrete distribution, when you given samples from a uniform distribution.

Let's assume that we are given a single sample of random variable U, uniformly distributed in the unit interval [0,1) (e.g. U = numpy.random.rand()). The goal is to generate samples from a non-uniform discrete distribution $P$ . We will assume that $P$ is a rational distribution. i.e. for any symbol $s$ , $P (s) = n_{s} / M$ , where $n_{s}, M$ are integers.

[5 points] Given a non-uniform rational distribution, we can sample a single random value $X_{1} \sim P$ from U by finding the cumulative distribution bin in which the sample U falls since the cumulative distribution also lies between [0,1). For example, if $P$ is the distribution such as P = {A: 2/7, B: 4/7, C: 1/7}, then we output the symbols A,B,C based on the intervals in which they lie as follows:
```
if U in [0.0, 2/7) -> output A
if U in [2/7, 6/7) -> output B
if U in [6/7, 1.0) -> output C
```
Generalize the above algorithm to any given rational distribution, and describe it in a few lines. For a distribution of alphabet size $k$ (e.g. $k = 3$ in the example above), what is the time/memory complexity of your algorithm wrt $k$ ?
[5 points] Complete the function generate_samples_vanilla in hw2_p2.py which takes in a non-uniform rational distribution P and returns data_size number of samples from it. You can assume that the distribution is given as a dictionary, where the keys are the symbols and the values are the frequency of occurrence in the data. For example, the distribution P = {A: 2/7, B: 4/7, C: 1/7} can be represented as P = Frequencies({'A': 2, 'B': 4, 'C': 1}). Ensure that your code passes the test_vanilla_generator test in hw2_p2.py. Feel free to add more test cases.
[5 points] Given a single sample of a uniform random variable U, how can you extend your algorithm in part 2.1 above to sample $n = 2$ i.i.d random values $X_{1}, X_{2} \sim P$ ? Provide a concrete algorithm for P= {A: 2/7, B: 4/7, C: 1/7}. Generalize your method to an arbitrary number of samples $n$ and describe it in a few sentences.
[5 points] Pulkit suggested that we can slightly modify Arithmetic Entropy Coder (AEC) we learnt in the class to sample a potentially infinite number of i.i.d samples $X_{1}, X_{2}, \dots, X_{n} \sim P$ given any rational distribution $P$ from a single uniform random variable sample U! You can look at Pulkit's implementation generate_samples_aec in hw2_p2.py to get an idea of how to exploit AEC. Can you justify the correctness of Pulkit's method in a few lines?

Note: Even though we say that we can sample potentially infinite number of samples, in practice we are limited by the precision of floats.
[5 points] Now let's say that you have to sample data $X_{0}, X_{1}, \dots, X_{n}$ from a Markov distribution $Q$ . Recall for a Markov Chain, $Q (X_{0}, X_{1}, \dots, X_{n}) = Q (X_{0}) Q (X_{1} ∣ X_{0}) \dots Q (X_{n} ∣ X_{n - 1})$ . Can you use your technique from Q2.3 or the technique suggested by Pulkit in Q2.4 to sample any number of samples $n$ with Markov distribution $Q$ from a single uniform random variable sample U in [0,1)? Describe the algorithm in a few lines.

Q3: Conditional Entropy (20 points)

In this problem we will get familiar with conditional entropy and its properties.

We learnt a few properties of conditional entropy in class:

$H (X) \geq H (X ∣ Y)$
$H (X, Y) = H (Y) + H (X ∣ Y)$

We will use these properties to show some other useful properties about conditional entropy and solve some fun problems!

[5 points] Let $f (X) = Z$ be an arbitrary function which maps $X \in X$ to a discrete set $Z \in Z$ . Then show that: $H (f (X) ∣ X) = 0$ . Can you intuitively explain why this is the case?
[5 points] Show that $H (f (X)) \leq H (X)$ , i.e. processing the data in any form is just going to reduce the entropy. Also, show that the equality holds if the function $f$ is invertible, i.e. if there exists a function $g$ such that $g (f (X)) = X$ . Can you intuitively explain why this is the case?
[4 points] In the HW1 of the 2023 edition of EE274, Pulkit and Shubham had an assignment to compress the Sherlock novel (lets call it $x_{or i g}$ ). Pulkit computed the empirical 0th order distribution of the letters and used those with Arithmetic coding to compress $x_{or i g}$ , and received average codelength $L_{1}$ . While working on the assignment, Shubham accidentally replaced all letters with lowercase (i.e A -> a, B -> b etc.). Lets call this modified text $x_{l o w erc a se}$ . Shubham compressed $x_{l o w erc a se}$ with the same algorithm as Pulkit, and got average codelength $L_{2}$ . Do you expect $L_{1} \geq L_{2}$ , or $L_{2} \geq L_{1}$ . Justify based on properties of Arithmetic coding and Q3.2.
[6 points] We say that random variables $X_{1}, X_{2}, \dots, X_{n}$ are pairwise independent, if any pair of random variables $(X_{i}, X_{j}), i \neq = j$ are independent. Let $X_{1}, X_{2}, X_{3}$ be three pairwise independent random variables, identically distributed as $B er (\frac{1}{2})$ . Then show that:
1. [3 points] $H (X_{1}, X_{2}, X_{3}) \leq 3$ . When is equality achieved?
2. [3 points] $H (X_{1}, X_{2}, X_{3}) \geq 2$ . When is equality achieved?
[NOT GRADED, THINK FOR FUN!] Let $Z_{1}, Z_{2}, \dots, Z_{k}$ be i.i.d $B er (\frac{1}{2})$ random variables. Then show that using the $Z_{i}^{'} s$ , you can generate $n = 2^{k} - 1$ pairwise independent random variables, identically distributed as $B er (\frac{1}{2})$ .

Q4: Bits-Back coding and rANS (45 points)

In class, we learnt about rANS. We started with the basic idea of encoding a uniform distribution on {0, ..., 9} (see Introduction section in notes) and then extended it to non-uniform distributions. In this problem we will look at a different way of thinking about rANS, which will help us understand the modern entropy coder.

Let's start by first generalizing our idea of encoding a uniform distribution on {0, ..., 9} to a uniform distribution on {0, ..., M-1}, where M can be thought of as number of symbols in the alphabet. The encoding works as following:

def encode_symbol(state, s, M):
    state = (state * M + s) 
    return state

The encoder maintains a single state, which we increase when we encode a symbol. Finally, we save the state by simply writing it out in the binary form. This function is implemented in hw2_p4.py as UniformDistEncoder.

[2 points] Write a decode_symbol pseudocode which takes in the encoded state state and M and returns the symbol s and the updated state state. Show that your decoder along with above encoding is lossless, i.e. we can recover the original symbol s from the encoded state state and M.
[3 points] Show that given data in {0, ..., M-1}, the encoder/decoder pair can be used to achieve lossless compression with ~ log2(M) bits/symbol as we encode large number of symbols.
[5 points] Now, implement your decoder in hw2_p4.py as UniformDistDecoder. Specifically, you just need to implement decode_op function. Ensure that your code passes the test_uniform_coder test in hw2_p4.py. Feel free to add more test cases.

Now, we want to implement a compressor which works well for non-uniform data. We will use the base encode/decode functions from UniformDistEncoder, UniformDistDecoder and approach this problem from a new perspective. In class, we learnt $H (X, Z) = H (X) + H (Z ∣ X)$ for any two random-variables $X$ and $Z$ . We will use this property to encode the data $X$ . Note that this identity implies $H (X) = H (X, Z) - H (Z ∣ X)$

Interpreting this intuitively, it should be possible to encode data X in following two steps:

a. Encode X,Z together using a joint distribution P(X,Z). Assuming an ideal compressor, this will require H(X,Z) bits.

b. Decode H(Z|X) from the encoded state using distribution P(Z|X). Again, assuming an ideal compressor, this lets us recover H(Z|X) bits.

Step b gives you an intuition for the question name -- bits-back! Here Z is an additional random variable typically latent variable (latent means hidden). Be careful while reading this step, as it is not a compressor for X but a decompressor for Z|X! This compressor assumes knowledge of X and decodes Z from the encoded state. More concretely, we will have an encoder-decoder pair which will work as follows:

def encode_symbol(state, X):
    state, Z = decode_zgx(state, X) # decode Z|X from state; knows X. returns Z and updated state.
    state = encode_xz(state, (X, Z)) # use this Z, and known X, to encode X,Z together. returns updated state.
    
    return state


def decode_symbol(state):
    state, (X, Z) = decode_xz(state) # decode X,Z from state. returns X,Z and updated state.
    state = encode_zgx(state, Z, X) # encode Z|X by updating state; knows X. returns updated state.
    
    return state, X

Note that how the encode step now involves both a decoding and an encoding step from another compressor! This is one of the key idea behind bits-back coding. We will now implement the above encoder/decoder pair for non-uniform data.

To see the idea, let's work out a simple case together. As usual let's assume that the non-uniform input is parametrized by frequencies freq_list[s] for s in {1,..,num_symbols} and M = sum(freq_list). For instance, if we have 3 symbols A,B,C with probabilities probs = [2/7, 4/7, 1/7], then we can think of frequencies as freq_list = [2,4,1] and M = 7. We can also create cumulative frequency dict as we saw in class, i.e. cumul = {A: 0, B: 2, C: 6}.

We will assume Z to be a uniform random variable in {0, ..., M-1}. Then, we can think of X as a function of Z as follows:

def X(Z):
    for s in symbols:
        if cumul(s) <= Z < cumul(s) + freq_list[s]:
            return s

i.e. X is the symbol s such that Z lies in the interval [cumul(s), cumul(s)+freq_list[s]). This is shown in the figure below for the example above.

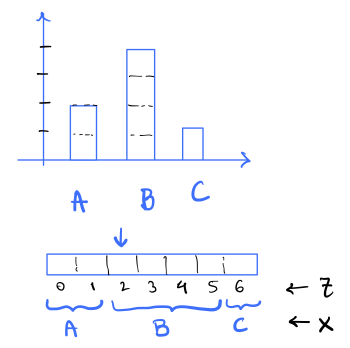
BB_ANS_1

For example if Z = 4, then X = B as cumul(B) = 2 <= 4 < 6 = cumul(B) + freq_list[B].

[2 points] What are the values of $H (X), H (Z), H (X ∣ Z)$ in the above example?
[3 points] What is the distribution and entropy of $Z$ given $X$ , i.e. $P (Z ∣ X)$ and $H (Z ∣ X = x)$ in the above example? Note that $H (Z ∣ X = x)$ is a function of x and hence you need to report it for each symbol x in the alphabet A,B,C.

Now, let's implement the encoder/decoder pair for the above example. We will use the following notation:

state is the encoded state
s is the symbol to be encoded (X)
freq_list is the list of frequencies of the symbols
We want to code the above scheme utilizing the joint compressors over X, Z (where Z is the latent variable). Z is uniformly distributed in {0, ..., M-1}.
- combined_symbol is the joint random variable Y = (X, Z). In our example, we only need to encode Z as X is a deterministic function of Z, i.e. combined_symbol = Z and will be in {0, ..., M-1}. For above example, say we want to encode Y = (B, 4), then we only need to encode Z = 4 as X=B is implied.
- fake_locator_symbol is the value of Z|X=x relative to cumul(x). This is a function of X=x. For above example of X = B, Z|X=B can be {2, 3, 4, 5} and hence fake_locator_symbol can be {0, 1, 2, 3} respectively as cumul(B) = 2.
- Therefore, combined_symbol and fake_locator_symbol allows us to have encoder/decoder pair for both (X,Z) and Z|X. Continuing our example, if we were to encode Y = (X=B, Z=4), we will encode it as combined_symbol = 4 and fake_locator_symbol = 2. Conversely, if we were to decode combined_symbol = 4, we will decode it as Y = (Z=4, X=B) and infer that fake_locator_symbol=2.

[5 points] We have implemented the encode_symbol function for NonUniformDistEncoder. Looking at the pseudocode above and the example, explain briefly how it works. Specifically, explain how encode_symbol achieves the relevant decode_zgx and encode_xz functions given in pseudocode in the context of example above.
[10 points] Now implement the decode_symbol function for NonUniformDistEncoder. You can use the encode_op and the decode_op from uniform distribution code. Ensure that your code passes the test_non_uniform_coder test in hw2_p4.py. Feel free to add more test cases.
[5 points] Show that for a symbol s with frequency freq[s], the encoder uses ~ log2(M/freq[s]) bits and is hence optimal.

Great, we have now implemented a bits-back encoder/decoder pair for a non-uniform distribution. Let us now see how it is equivalent to rANS we studied in class. As a reminder, the rANS base encoding step looks like

def rans_base_encode_step(x,s):
   x_next = (x//freq[s])*M + cumul[s] + x%freq[s]
   return x_next

[5 points] Justify that encode_symbol in NonUniformDistEncoder performs the same operation as above.

Similarly, as a reminder, the rANS base decoding step looks like

def rans_base_decode_step(x):
   # Step I: find block_id, slot
   block_id = x//M
   slot = x%M
   
   # Step II: Find symbol s
   s = find_bin(cumul_array, slot) 
   
   # Step III: retrieve x_prev
   x_prev = block_id*freq[s] + slot - cumul[s]

   return (s,x_prev)

[5 points] Justify that decode_symbol in NonUniformDistEncoder performs the same operation as above.

Therefore, bits-back coding is equivalent to rANS! Thinking again in terms of $H (X) = H (X, Z) - H (Z ∣ X)$ , it allows us to interpret rANS in terms of latent variables $Z$ in a more intuitive way. This question was highly motivated by the IT-Forum talk by James Townsend in 2022. Check out the YouTube video if you are interested to learn more!

Submission Instructions

Please submit both the written part and your code on Gradescope in their respective submission links. We will be using both autograder and manual code evaluation for evaluating the coding parts of the assignments. You can see the scores of the autograded part of the submissions immediately. For code submission ensure following steps are followed for autograder to work correctly:

As with HW1, you only need to submit the modified files as mentioned in the problem statement.
- Compress the HW2 folder into a zip file. One way to obtain this zip file is by running the following zip command in the HWs folder, i.e.
```
cd HWs
zip -r HW2.zip HW2
```
  Note: To avoid autograder errors, ensure that the directory structure is maintained and that you have compressed HW2 folder containing the relevant files and not HWs folder, or files inside or something else. Ensure the name of the files inside the folder are exactly as provided in the starter code, i.e. hw2_p2.py, hw2_p4.py etc. In summary, your zip file should be uncompressed to following directory structure (with same names):
```
HW2
├── hw2_p1.py
├── hw2_p2.py
└── hw2_p4.py
```
Submit the zip file (HW2.zip obtained above) on Gradescope Programming Part Submission Link. Ensure that the autograded parts runs and give you correct scores.

Before submitting the programming part on Gradescope, we strongly recommend ensuring that the code runs correctly locally.