EE274 (Fall 25): Homework-3

Focus area: Context-based compression and LZ77
Due Date: Nov 11, midnight (11:59 PM)
Weightage: 15%
Total Points: 150
Submission Instructions: Provided at the end of HW (ensure you read these!)
Submission link:
- For written part (110): HW3-Written
- For programming part (40): HW3-Code

Please ensure that you follow the Stanford Honor Code while doing the homework. You are encouraged to discuss the homework with your classmates, but you should write your own solutions and code. You are also encouraged to use the internet to look up the syntax of the programming language, but you should not copy-paste code from the internet. If you are unsure about what is allowed, please ask the instructors.

Note for the coding part
Before starting the coding related questions ensure following instructions from HW1 are followed:

Ensure you are using the latest version of the SCL EE274/HWs GitHub branch. To ensure run the following command in the SCL repository you cloned from HW1:
```
git status
```
You should get an output saying On branch EE274_Fall25/HWs. If not, run the following command to switch to the correct branch:
```
git checkout EE274_Fall25/HWs
```
Finally ensure you are on the latest commit by running:
```
git pull
```
You should see a HW3 folder in the HWs folder.
Ensure you are in the right conda environment you created in HW1. To ensure run the following command:
```
conda activate ee274_env
```
Before starting, ensure the previous tests are passing as expected. To do so, run following from stanford_compression_library folder:
```
find scl -name "*.py" -exec py.test -s -v {} +
```
and ensure tests except in HW folders pass.

Q1 LZ77 compression for small data (35 points)

In this problem, we will understand how LZ77 compression performs on small files and how to improve its performance. Recall that the LZ77 algorithm looks for matches in a window storing the previously seen data and then encodes the match lengths, match offsets and unmatched characters (literals). We use the LZ77 implementation provided in SCL for the experiments below, and you can take a look at the code here to understand the details better. We have provided a set of small json files in the p1_data/github_data directory. Run the script python hw3_p1.py -i p1_data/github_data in scl/HWs/HW3 folder, which produces the following output:

Compressing without using a seed input
Number of files: 134
Total uncompressed size (in bits): 956272
Normalized uncompressed size (in avg. bits/file): 7136
Total size after compressing the files individually (in bits): 363774
Total size after compressing the files jointly (in bits): 71795

Ignore the first line for a moment. We see that we have 134 relatively small files with average size of 7136 bits. If we compress the files individually and then sum the sizes, we get a total of 363774 bits, whereas if we concatenate the files and then compress them as a single block ("jointly") the compressed size is just 71795 bits!

[4 points] Give two reasons why concatenating the files together provides a reduction in file size.

HINT: One of the reasons is applicable even if the files were from completely distinct sources and had no similarity whatsoever.

Ideally one would just combine these small files into bigger batches for the best compression. However, we sometimes need to store, transmit or compress small files. For example, we need to transmit short JSON messages/network packets between servers where latency is important, and we can't batch requests. Another common use case is when databases use small data pages for fast random access. Small files also show up when we are working with resource constrained devices that cannot hold large files.

To improve the compression on small files, we consider a slight modification of the LZ77 algorithm we studied in class. Both the compressor and the decompressor now take an additional seed input, which is just a sequence of bytes. The idea is simple: instead of starting the LZ77 compressor with an empty window, we instead initialize the window with a seed input (and appropriately update the other indexing data structures). The same seed input should be used during compression and decompression to enable recovery.

The overall system architecture needs to maintain these seed inputs (which might be specific to particular data categories), and make sure the encoders and decoders can access these. The seed inputs are usually constrained to be small to avoid extra overhead.

We provide a sample seed input for the above dataset in p1_data/github_data_seed_input.txt. Run python hw3_p1.py -i p1_data/github_data -s p1_data/github_data_seed_input.txt to obtain the following:

Loading seed input from p1_data/github_data_seed_input.txt
Number of files: 134
Total uncompressed size (in bits): 956272
Normalized uncompressed size (in avg. bits/file): 7136
Total size after compressing the files individually (in bits): 224738
Total size after compressing the files jointly (in bits): 70678

[6 points] We see a significant reduction in the total size for compressing the files individually (363774 bits to 224738 bits). Based on your understanding of the LZ77 algorithm and your answer to Q1.1, explain why this is the case. You might find it useful to look both at the json files in p1_data/github_data/ and the seed input in p1_data/github_data_seed_input.txt.
[2 points] Why is the impact of using the seed input negligible when we compress the files jointly?
[3 points] The provided seed input file is less than 1 KB in size. If you were allowed to choose an arbitrarily large seed input, how might you design it to minimize the compressed size for this specific dataset.

HINT: Think about the best case scenario for LZ77 parsing - longest possible matches and no literals.
[10 points] Now you will create a seed input for another dataset provided in the p1_data/pokemon_data directory. We will evaluate your submissions on a test dataset which has similar files as the p1_data/pokemon_data directory. Your submission should satisfy the following:
- name the seed input file as p1_data/pokemon_data_seed_input.txt
- the seed input file should be less than 1 KB (1000 B) large. You can check the file size in bytes by running wc -c p1_data/pokemon_data_seed_input.txt.
- the total size for compressing the files individually should reduce to at least 2x when using the seed input (vs. when not using a seed input) for both the pokemon_data set and the autograder submission. For example, if the Total size after compressing the files individually is 308031 bits without seed input, then with your seed input it should be at most 154015 bits.
- A couple hints to help you achieve best results: (i) try to use similar JSON format and formatting in your seed input file as in the pokemon data files - this includes using the same 2-space indendation, and (ii) (for Windows users) make sure your seed input uses LF (\n) line-endings and not CRLF (\r\n) - verify your editor is not changing this automatically.
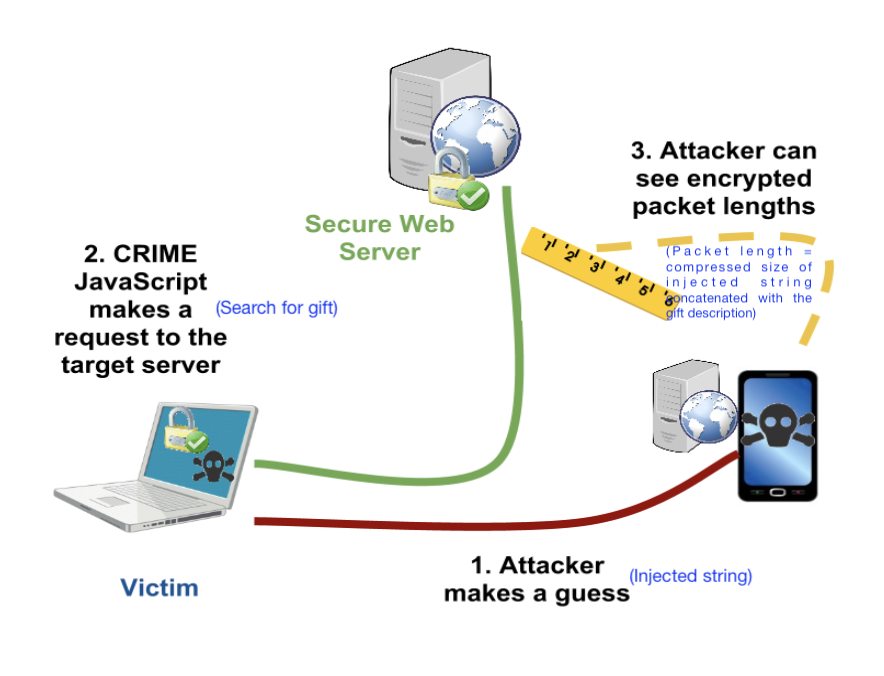
[10 points] Christmas is approaching and Jim knows that Della is going to buy a thoughtful gift for him. Unable to control his curiosity and being a part-time hacker, he has decided to spy on Della’s internet search patterns by executing a side-channel attack. As shown in the diagram below, he is able to inject strings into Della’s http requests, and once Della makes a search request he can monitor the LZ77 compressed size of the response. Here the response includes his injected string along with the gift description, allowing him to infer some side-channel information about the search. Don't take the story too seriously from a internet security standpoint! But do take a look at the references provided in the note below to learn more about real instances of such attacks.

Use the provided webpage to help Jim select injected strings and based on that make a guess about the chosen gift. Include a screenshot of the injected strings you used and the “🎉 Correct!” message.

Note:

To learn more about small data compression using seed inputs and how it is used in practice, you can have a look at Yann Collet's IT-forum talk (Part 1, Part 2).
zstd uses the term "dictionary" to refer to what we called seed inputs above.
To read more about LZ77 side-channel attacks mentioned in part 6, you can refer to the slides here or Fall 2023 course project report here.

Q2: Burrows Wheeler Transform and compression (50 points)

DISCLAIMER: This problem looks longer but is actually simpler :P

You might be familiar with Fourier transforms, DCT transform, wavelet transform, etc. for images and audio signals. These transforms are widely used as they are invertible and make the data easier to analyse, compress, etc.

In this problem, we will learn about a few lossless transforms for textual data, which have been used for various applications, including data compression.

I. The BWT algorithm:

In 1994, David Wheeler and Michael Burrows discovered (co-incidentally at the DEC Research Labs in Palo Alto!) an invertible transform for textual data, which supposedly made the data easier to compress. In this question, we will learn more about the BWT algorithm and its properties.

The BWT forward transform works the following way:

STEP-I

Let's say you are given a sequence BANANA. The first thing you do is add a delimiter ~ to the end. Thus, our new sequence is now: BANANA~. Note that the delimiter is a unique character we are sure never occurs in the input sequence, and is useful to mark the ending of our sequence
STEP-II

In the next step, we form all cyclic rotations of the word BANANA~. As the sequence length is n=7, we will have 7 such rotations.
```
Input string: BANANA
# all cyclic rotations
BANANA~
~BANANA
A~BANAN
NA~BANA
ANA~BAN
NANA~BA
ANANA~B
```
STEP-III

Sort these strings lexico-graphically. This results in n permutations of a string of length n resulting in a n X n 2D table — called a Burrows Wheeler's Matrix (BWM). The 7 X 7 BWM for our example is shown below:
```
# sorted strings
ANANA~B
ANA~BAN
A~BANAN
BANANA~
NANA~BA
NA~BANA
~BANANA
```
STEP-IV

Now consider the string formed by last letters of the sorted strings. This new string is the BWT transform of the input!
```
BANANA -> BNN~AAA
```

[5 points] Here are some other examples of BWT:
```
BANANA -> BNN~AAA
abracadabraabracadabraabracadabra -> rrdd~aadrrrcccraaaaaaaaaaaabbbbbba
hakunamatata -> hnmtt~aauaaka
```
Notice that the BWT forward transform of x_input = BANANA -> BNN~AAA has the letters of BANANA~ permuted, i.e. BWT(x_input) is just reordering the letters in the input in a particular way. Justify in a few lines why BWT(x_input) is a permutation of the string x_input~ (x_input~ -> x_input concatenated with the delimiter ~).
[5 points] Manually compute and show the BWT transform for PANAMA, using the method above. Show your work to get credit (that is you can't just write the final transform but show the steps described above).
[10 points] Implement the BWT (forward) transform in the hw3_p2.py file, BurrowsWheelerTransform::forward function. Remember to add a delimiter in the input string (you can use ~ as delimiter as ~ has the highest ascii value). You may use the test_bwt_transform() (by commenting out the inverse bwt part) to test your implementation. What is the time complexity of your BWT forward transform implementation for an input of length n?

II. The Inverse BWT Algorithm

The surprising part is that BWT is actually a fully invertible transform, i.e. we can fully retrieve back the original input from the BWT transform e.g. we can recover input string BANANA~ from the BWT transform BNN~AAA. The inverse transform works by retrieving the Burrows Wheeler Matrix (BWM) one column at a time. The inverse BWT proceeds in the following way:

In the beginning we only have the BWT transform which is the last column of the BWM. We show the BWT transform and the BWM below.
```
# STEP-0
------B
------N
------N
------~
------A
------A
------A
```
Notice that each column is a permutation of BANANA~. As the rows of BWM are lexicographically sorted, we can retrieve the first column on BWM by sorting the last column.
```
# STEP-1
A-----B
A-----N
A-----N
B-----~
N-----A
N-----A
~-----A
```

Due to the cyclic rotations which we used to form the BWM, we can now copy over the last column to the beginning, and we have the first two letters for each row of BWM (although in the incorrect order). We can sort these rows to get the first two columns of the BWM.

# STEP-2
A-----B  -> BA-----                   AN-----
A-----N  -> NA-----                   AN-----
A-----N  -> NA-----                   A~-----
B-----~  -> ~B-----   ===> SORT ===>  BA-----
N-----A  -> AN-----                   NA-----
N-----A  -> AN-----                   NA-----
~-----A  -> A~-----                   ~B-----

We can now repeat the procedure, since we know the last column is the BWT transformed string:

# STEP 1,2 (repeated)
AN----B  -> BAN----                   ANA----
AN----N  -> NAN----                   ANA----
A~----N  -> NA~----                   A~B----
BA----~  -> ~BA----   ===> SORT ===>  BAN----
NA----A  -> ANA----                   NAN----
NA----A  -> ANA----                   NA~----
~B----A  -> A~B----                   ~BA----

Continuing, this way, we can retrieve the full BWM, and then just pick the row which ends with ~
```
# BWM
ANANA~B
ANA~BAN
A~BANAN
BANANA~    ===> BANANA~  ---> :D
NANA~BA
NA~BANA
~BANANA
```

[5 points] Manually compute the inverse of TGCA~AA. Show your work to get credit (that is you can't just write the final inverse transform but show the steps described above).
[10 points] Implement the BWT inverse transform in hw3_p2.py in the BurrowsWheelerTransform::inverse function. Please add (some) inline comments describing your algorithm. What is the time, memory complexity of your BWT inverse transform implementation for an input of length n?

[5 points] Notice that the BWT forward transform of typical english language words/sentences have lots of consecutive repeated letters. For example:

# BWT forward transforms of some english words
BANANA -> BNN~AAA
abracadabraabracadabraabracadabra -> rrdd~aadrrrcccraaaaaaaaaaaabbbbbba
hakunamatata -> hnmtt~aauaaka

# first 300 letters of sherlock novel
The Project Gutenberg eBook of The Hound of the Baskervilles, by Arthur Conan DoyleThis eBook is for the use of anyone anywhere in the United States andmost other parts of the world at no cost and with almost no restrictionswhatsoever. You may copy it, give it away or re-use it under the termsof the
-->
yernteedfe.htsfedt,yosgs,ekeeyuttkedsytrroefnrrfftedester  ee       ~e   n    pB th mwn   eielnnnnhhhhnrvsshhhr  ljtthdvhbtktlrohooooo r twtTTtttttwtTtrv th    nwgooosrylia ldraioeuauaoU  oaanns    srooCyiBBc fwcmm YHD oueoeoee  etoePAaeeiiteuuatmoooencsiassiiSiu ai     o rcsraoo h- Gierasy  bapaonne

So in a way BWT forward transform is approximately sorting the input strings. Can you think of why BWT has this property?

HINT: In the BWM, the last column forms the BWT while the first $n - 1$ columns form suffixes of the last column. For example, if the last entry in a particular row is $x_{j}$ ( $j$ th value in original string), then the first $n - 1$ entries in that row would be the cyclic suffix: $x_{j + 1} \dots x_{n} x_{1} \dots x_{j - 1}$ Given the rows are sorted lexicographically, what can you say about the suffixes of nearby entries in the BWT?

III. Using BWT for compression

As we saw in previous part, BWT tends to club letters of the input string together. We will use this property to see if we can improve compression. To do this, we also implement another invertible transform called the Move to Front (MTF) transform. The Move To Front transform keeps a table of the symbols in the data, and moves the most recent symbol to the top of the table. The transform output is the index of the symbols in this changing table and thus the symbols that are more frequent in a local context get a lower index. The MTF forward and inverse transforms are already implemented and included in hw3_p2.py and are described quite well in the wikipedia article here: https://en.wikipedia.org/wiki/Move-to-front_transform.

Here are some sample outputs on applying MTF transform:

Input str: aaabbbaaacccaaa
MTF: [97, 0, 0, 98, 0, 0, 1, 0, 0, 99, 0, 0, 1, 0, 0]

Input str: rrdd~aadrrrcccraaaaaaaaaaaabbbbbba
MTF: [114, 0, 101, 0, 126, 100, 0, 2, 3, 0, 0, 102, 0, 0, 1, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 102, 0, 0, 0, 0, 0, 1]

We use the BWT, MTF transforms to transform the first 50,000 characters (let's call this the input_data) of our sherlock novel and analyze the entropy of the empirical distribution of the transformed string. (this output can be obtained by running the test test_bwt_mtf_entropy if you are curious!). The output obtained is as below:

Input data: 0-order Empirical Entropy: 4.1322
Input data + BWT: 0-order Empirical Entropy: 4.1325
Input data + MTF: 0-order Empirical Entropy: 4.6885
Input data + BWT + MTF: 0-order Empirical Entropy: 2.8649

[10 points] Let's try to understand the compression results above a bit better:
1. Given a good implementation of an Arithmetic coder, what is approximate average codelength per symbol you might expect on compressing the input_data using its empirical 0-order distribution (i.e. just the symbol counts)?
2. Notice that the empirical entropy of input_data is almost the same as that of bwt_data = BWT(input_data). In fact the empirical entropy of bwt_data is slightly higher than that of input_data (4.1325 vs 4.1322). Justify why is this the case.
3. Notice that empirical entropy of mtf_bwt_data = MTF(BWT(input_data)) is much lower than that of the input_data (2.8649 vs 4.1322). Can you think of why this is the case?
4. Based on the numbers you have, describe a compression scheme which achieves average codelength of approximately ~2.87 bits/symbol on the input_data. You don't need to implement this compressor, but ensure you clearly describe the steps involved in encoding and decoding. You are free to use any compressors you have learnt in the class.
Feel free to experiment with the test functions, to print transformed data or to build better intuition with custom examples. Please include any relevant outputs in your submission which you found useful to answer these questions.

NOTE: compressors such as bzip2, and bsc in fact use BWT and MTF transforms along with a few other tricks to obtain great compression. BWT algorithms have also found another surprising use: they allow efficient searching over compressed text! Here are more references in case you are interested:

bzip2, bsc
wikipedia article: https://en.wikipedia.org/wiki/Burrows%E2%80%93Wheeler_transform
BWT for searching over compressed text: slides

Q3: Compression with side information (20 points)

Let's consider a simple puzzle:

Let $X$ be a 3 bit random variable where each bit is i.i.d $B er (0.5)$ , i.e. $X$ is uniformly distributed in ${000, 001, 010, 011, 100, 101, 110, 111}$ with probability $1/8$ ,
and $Y = X \oplus e$ , where $e \in {000, 001, 010, 100}$ and is independent of $X$ . The distribution of $e$ is unknown, i.e. $Y$ can be different from $X$ in at most one bit position. Recall that $\oplus$ is the bitwise-XOR operation.

[5 points] Show that $H (X) = 3, H (X ∣ Y) \leq 2$ .

HINT: Consider $H (X, e ∣ Y)$ and write it in two different ways
[5 points] Kakashi wants to losslessly encode $X$ and send the encoded coderword to Sasuke. What is the optimal compression scheme for Kakashi?
[5 points] Now let's say both Kakashi and Sasuke have access to $Y$ , i.e. $Y$ is the side-information available to both Kakashi and Sasuke (through side-information ninjutsu :P). In that case, show that Kakashi can do better than in Q3.2, by using 2 bits to transmit $X$ .
[5 points] Unfortunately Kakashi lost access to $Y$ , and only knows $X$ but Sasuke still has access to the side information $Y$ . Show that in this case Kakashi can still losslessly encode $X$ and send it to Sasuke using 2 bits, i.e. surprisingly we just need the side-information at the decoder, and not necessarily at the encoder.

NOTE: It is quite fascinating that we need side-information only at the decoder. This property can be generalized to more general scenarios, and is the foundation for distributed data compression. E.g. see Slepian-Wolf coding and Wyner-Ziv coding for more details.

Q4: kth order adaptive arithmetic coding (40 points)

Shubham wants to test the compression performance of the k-th order context models using Arithmetic Coding he has implemented. However, one problem is that for unknown sources it is very difficult to compute the fundamental limit on the average codelength. So, he decides to test his algorithms on a synthetic dataset.

He generates data using a noisy version of Linear Feedback Shift Register based Pseudorandom generator. The name sounds quite complicated, but it is a simple concept (you don't need to know anything about it to attempt this problem). The pseudocode to generate noisy-LFSR sequence is given below (also given in HW code hw3_p4.py):

def pseudo_random_LFSR_generator(data_size, tap, noise_prob=0):
    # initial sequence = [1,0,0,0,...] of length tap
    initial_sequence = [1] + [0] * (tap - 1)

    # output sequence
    output_sequence = list(initial_sequence)
    for _ in range(data_size - tap):
        s = output_sequence[-1] ^ output_sequence[-tap]  # xor
        if noise_prob > 0: 
            s = s ^ Bernoulli(p=noise_prob) # add noise
        output_sequence.append(s)
    return output_sequence

Our pseudo_random_LFSR_generator generates an output sequence of length data_size. At each step, it calculates the next bit using XOR (a ^ b is True/1 if exactly one of a and b is True/1) between the last bit in the sequence and the bit located tap positions before it (this simulates LFSR behavior). Optionally, if noise_prob is greater than 0, it adds noise to the calculated bit by XOR-ing it with a random binary value generated with a given probability (noise_prob). The calculated (possibly noisy) bit is appended to the sequence in each iteration. To initialize the sequence, we always start it with [1,0,0,0,...] so that we have tap number of bits available to calculate the next bit.

For concreteness let's take a specific parameter setting (function in hw3_p4.py):

pseudo_random_LFSR_generator(data_size=10000, tap=3, noise_prob=0)

We see that the first 12 symbols of the sequence looks like:

1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, ...

Notice that the sequence looks random-ish but starts repeating after 8 symbols. In fact if we look at the first 7 3-mers (substrings of length 3), i.e. 100, 001, ..., 010, then we see that they are all unique and do not repeat! The LFSR sequence with noise_prob=0, is in fact a simple pseudo-random generator used in the past. We will use this source to further our understanding of context based compression.

Let's start by defining the $k^{th}$ order empirical entropy of the sequence. Recall, if your sequence is $x_{0}, x_{1}, x_{2}, \dots, x_{n}$ , the $k^{th}$ -order empirical entropy of the sequence can be computed by making a joint and conditional probability distribution table using counts of the previously seen symbols (we saw this in class in L9 on context based AC lecture). Specifically, assuming the alphabet is $X$ , for any $(x_{0}, x_{1}, x_{2}, \dots x_{k}) \in X^{k + 1}$ , we can define the empirical joint probability as: $p (x_{0}, x_{1}, x_{2}, \dots x_{k}) = \frac{count ( x _{0} , x _{1} , x _{2} , \dots x _{k} )}{total count of k+1-tuples}$

the empirical conditional probability as: $p (x_{k} ∣ x_{0}, x_{1}, x_{2}, \dots x_{k - 1}) = \frac{p ( x _{0} , x _{1} , x _{2} , \dots x _{k} )}{p ( x _{0} , x _{1} , x _{2} , \dots x _{k - 1} )} = \frac{p ( x _{0} , x _{1} , x _{2} , \dots x _{k} )}{\sum _{x^{'} \in X} p ( x _{0} , x _{1} , x _{2} , \dots x _{k - 1} , x ^{'} )}$

and the $k^{th}$ -order empirical entropy is then given by summing over all possible $(k + 1)$ -tuples:

$H_{k} (X) = (x_{0}, x_{1}, x_{2}, \dots, x_{k}) \in X^{k + 1} \sum p (x_{0}, x_{1}, x_{2}, \dots, x_{k}) lo g \frac{1}{p ( x _{k} ∣ x _{0} , x _{1} , x _{2} , \dots , x _{k - 1} )}$

[5 points] Show that for infinite data ( $n \to \infty$ ) and $k_{1} > k_{2}$ , $H_{k_{1}} (X) \leq H_{k_{2}} (X)$ i.e. $k_{1}^{th}$ -order empirical entropy is always less than (or equal to) $k_{2}^{th}$ -order empirical entropy.

You can assume the data distribution is stationary and ergodic (or in simple words you can assume the empirical probabilities converge to the stationary distribution).
[10 points] Next let's calculate $H_{k} (X)$ for the above given sequence with tap=3, noise_prob=0. (Recall the sequence from above: 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, ...)
1. Compute the $0^{th}$ order count-distribution and empirical entropy of the sequence. HINT: sequence repeats itself!
2. Compute the $1^{st}$ order count-distribution and empirical entropy of the sequence.
3. Finally, argue that for $k \geq 3$ , the $k^{th}$ -order empirical entropy of the sequence is 0.
[5 points] Now, Shubham decides to use Adaptive Arithmetic coding to compress data from this source. For the case with no added noise (noise_prob=0), the number of bits/symbol we achieve is as follows for different context size k. You can use the test code in hw3_p4.py to generate these numbers by changing and choosing appropriate parameters. Use the -s flag in pytest to dump the output even for successful tests.
```
----------
Data generated as: X[n] = X[n-1] ⊕ X[n-3]
data_size=10000
AdaptiveArithmeticCoding, k=0, avg_codelen: 0.989
AdaptiveArithmeticCoding, k=1, avg_codelen: 0.969
AdaptiveArithmeticCoding, k=2, avg_codelen: 0.863
AdaptiveArithmeticCoding, k=3, avg_codelen: 0.012
AdaptiveArithmeticCoding, k=4, avg_codelen: 0.011
AdaptiveArithmeticCoding, k=7, avg_codelen: 0.011
AdaptiveArithmeticCoding, k=15, avg_codelen: 0.012
AdaptiveArithmeticCoding, k=22, avg_codelen: 0.013
```
Argue why these results make sense. In particular, argue that Adaptive Arithmetic coding with order k=0,1,2 cannot do much better than 1 bit/symbol. Also, argue that for k >= 3, the compression should be ~0 bits/symbol.

Next, Shubham decides to encode noisy-LFSR sources with noise_prob=0.01 and TAP=3,7,15. The noisy LFSR is very similar to the non-noisy version, except we add a bit of noise after xoring the two past symbols as shown in the pseduo-code above.

[5 points] For TAP=3, noise_prob=0.01, what is the fundamental limit to which you can compress this sequence, i.e. what is $k^{th}$ -order empirical entropy of the sequence for $k \geq 3$ and large $n$ ?

[5 points] Next, we encode noisy-LFSR sequence with parameters noise_prob=0.01 and TAP=3,7,15 using Adaptive Arithmetic coding. The number of bits/symbol we achieve is as follows for different context size k. You can again use the test code in hw3_p4.py to generate these numbers by changing and choosing appropriate parameters. In these cases we observe the following average codelength, for a sequence of length 10000

----------
Data generated as: X[n] = X[n-1] ⊕ X[n-3] ⊕ Bern_noise(0.01)
DATA_SIZE=10000
AdaptiveArithmeticCoding, k=0, avg_codelen: 1.003
AdaptiveArithmeticCoding, k=1, avg_codelen: 1.002
AdaptiveArithmeticCoding, k=2, avg_codelen: 0.999
AdaptiveArithmeticCoding, k=3, avg_codelen: 0.087
AdaptiveArithmeticCoding, k=4, avg_codelen: 0.089
AdaptiveArithmeticCoding, k=7, avg_codelen: 0.097
AdaptiveArithmeticCoding, k=15, avg_codelen: 0.121
AdaptiveArithmeticCoding, k=22, avg_codelen: 0.146
AdaptiveArithmeticCoding, k=24, avg_codelen: 0.152

----------
Data generated as: X[n] = X[n-1] ⊕ X[n-7] ⊕ Bern_noise(0.01)
DATA_SIZE=10000
AdaptiveArithmeticCoding, k=0, avg_codelen: 1.004
AdaptiveArithmeticCoding, k=1, avg_codelen: 1.004
AdaptiveArithmeticCoding, k=2, avg_codelen: 1.005
AdaptiveArithmeticCoding, k=3, avg_codelen: 1.007
AdaptiveArithmeticCoding, k=4, avg_codelen: 1.009
AdaptiveArithmeticCoding, k=7, avg_codelen: 0.139
AdaptiveArithmeticCoding, k=15, avg_codelen: 0.192
AdaptiveArithmeticCoding, k=22, avg_codelen: 0.240
AdaptiveArithmeticCoding, k=24, avg_codelen: 0.254

----------
Data generated as: X[n] = X[n-1] ⊕ X[n-15] ⊕ Bern_noise(0.01)
DATA_SIZE=10000
AdaptiveArithmeticCoding, k=0, avg_codelen: 1.004
AdaptiveArithmeticCoding, k=1, avg_codelen: 1.004
AdaptiveArithmeticCoding, k=2, avg_codelen: 1.005
AdaptiveArithmeticCoding, k=3, avg_codelen: 1.006
AdaptiveArithmeticCoding, k=4, avg_codelen: 1.008
AdaptiveArithmeticCoding, k=7, avg_codelen: 1.031
AdaptiveArithmeticCoding, k=15, avg_codelen: 0.949
AdaptiveArithmeticCoding, k=22, avg_codelen: 0.955
AdaptiveArithmeticCoding, k=24, avg_codelen: 0.957

Notice that the average codelength for TAP=3,7 is at its minima for k=TAP value and then increases as we further increase k which seems to suggest the result we saw in Q4.1 is wrong. Argue:

Why do these results still make sense and do not contradict theory?
For TAP=15, even for context size k=15, why is the model not able to compress the data very well?

[10 points] Instead of using Adaptive Arithmetic coding, Jiwon suggested that if we know the source parameters (i.e. TAP and noise_prob), then we could predict a better probability distribution of the next symbol based on the past, and use this for performing Arithmetic coding. Jiwon thinks this implementation should work for arbitrary values of TAP and input sequence lengths. Complete Jiwon's update_model logic in NoisyLFSRFreqModel provided in hw3_p4.py. For the first TAP symbols you can use arbitrary predictions (e.g., uniform distribution) without affecting the results for large sequences.

Once you have implemented the model, run the tests (py.test -s hw3_p4.py) for TAP=3,7,15 and noise_prob=0.01 again and report the average codelength obtained for the LFSR model. How do these results compare with the Adaptive Arithmetic coding results (from part 5) and to the expected theoretical limit (from part 4)? Explain why this is the case.

NOTE: References provided with Lecture 9 on Context-based Arithmetic Coding will be useful in attempting this problem (SCL implementation of adaptive arithmetic coding, notes, slides, etc.)

Q5: HW3 Feedback (5 points)

Please answer the following questions, so that we can adjust the difficulty/nature of the problems for the next HWs.

How much time did you spent on the HW in total?
Which question(s) did you enjoy the most?
Are the programming components in the HWs helping you understand the concepts better?
Did the HW3 questions complement the lectures?
Any other comments?

Submission Instructions

Please submit both the written part and your code on Gradescope in their respective submission links. We will be using both autograder and manual code evaluation for evaluating the coding parts of the assignments. You can see the scores of the autograded part of the submissions immediately. For code submission ensure following steps are followed for autograder to work correctly:

As with HW1, you only need to submit the modified files as mentioned in the problem statement.
- Compress the HW3 folder into a zip file. One way to obtain this zip file is by running the following zip command in the HWs folder, i.e.
```
cd HWs
zip -r HW3.zip HW3
```
  Note: To avoid autograder errors, ensure that the directory structure is maintained and that you have compressed HW3 folder containing the relevant files and not HWs folder, or files inside or something else. Ensure the name of the files inside the folder are exactly as provided in the starter code, i.e. hw3_p1.py, hw3_p2.py etc. In summary, your zip file should be uncompressed to following directory structure (with same names):
```
HW3
├── p1_data
    └──pokemon_data_seed_input.txt
├── hw3_p1.py
├── hw3_p2.py
└── hw3_p4.py
└── sherlock_ascii.txt
```
Submit the zip file (HW3.zip obtained above) on Gradescope Programming Part Submission Link. Ensure that the autograded parts runs and give you correct scores.

Before submitting the programming part on Gradescope, we strongly recommend ensuring that the code runs correctly locally.