EE274 (Fall 25): Homework-4

• Focus area: Lossy compression
• Due Date: 12/02, Tue, midnight (11:59 PM)
• Weightage: 15%
• Total Points: 120

Q1: Mutual Information and Rate Distortion (20 points)

1. [5 points] Consider random variables $X$ and $Y$ and let $f$ be an arbitrary function applied to $Y$. Show that $$I(X;Y)\ge I(X;f(Y))$$ When does equality hold?

   Note: This is a special case of the data-processing inequality, which more generally holds whenever $X-Y-Z$ form a Markov chain (i.e., $X$ and $Z$ are conditionally independent given $Y$) and says that $I(X;Y)\ge I(X;Z)$. Intuitively, this says that no processing of $Y$, deterministic or random, can increase the information that $Y$ contains about $X$. You can't boost information about $X$ contained in $Y$ just by processing it further!

   Solution Because conditioning reduces entropy, we have $$H(X|f(Y))\ge H(X|Y,f(Y))$$ We also have $$H(X|Y,f(Y))=H(X|Y)$$ because $X$ and $f(Y)$ are conditionally independent given $Y$ (implying that $P(X|Y=y)=P(X|Y=y,f(Y)=f(y))$ which implies the equality). This is because $f(Y)$ is a function of $Y$ so knowing it does not provide any additional information about $X$ that $Y$ cannot already provide.

   Thus, we have $H(X|f(Y))\ge H(X|Y)$. Using the definition of mutual information: $$I(X;Y)=H(X)-H(X|Y)$$ $$I(X;f(Y))=H(X)-H(X|f(Y))$$

   Since $H(X|f(Y))\ge H(X|Y)$ and entropies are always positive, this implies that $I(X;Y)\ge I(X;f(Y))$. The same proof can be used for the more general case for the data-processing inequality.

   Equality holds when $H(X|f(Y))=H(X|Y,f(Y))=H(X|Y)$, which happens when $X$ and $Y$ are conditionally independent given $f(Y)$. Intuitively, this means that $f(Y)$ captures all the information about $X$ that is present in $Y$. For example, if $X=Y^2$ then choosing $f(Y)=|Y|$ will give equality since the square of $Y$ can be determined from its absolute value.

2. [15 points] Consider a source $X\sim i.i.d.Ber(\frac{1}{2})$ which we wish to lossily compress. The reconstruction $Y$ is allowed to take values in $\{0,1,e\}$ where $e$ represents an erasure symbol. The distortion function is given by $$d(x,y)=\{\begin{array}{l}0,y=x\\ 1,y=e\\ \infty ,\mathrm{otherwise}\end{array}$$ In words, erasures incur a distortion of $1$, but making a mistake is not allowed (infinite distortion).

   a. [10 points] Show that $R(D)={\min }_{E[d(x,y)]\le D}I(X;Y)=1-D$ for $D\in [0,1]$.

   Hint: You can first show that $I(X;Y)=H(X)-P(Y=e)H(X|Y=e)$ under the condition $E[d(x,y)]\le D$. Can you relate $P(Y=e)$ to $E[d(X,Y)]$?

   Solution For $X,Y$ in the feasible set where $Ed(X,Y)\le D$ we have $$\begin{array}{rl}I(X;Y)& =H(X)-H(X|Y)\\ & =1-[H(X|Y=0)P(Y=0)+H(X|Y=1)P(Y=1)+H(X|Y=e)P(Y=e)]\\ & =1-H(X|Y=e)P(Y=e)\\ & \ge 1-P(Y=e)\\ & \ge 1-D,\end{array}$$ where:

   1. the first line just uses the definition of mutual information.
   2. the second line expands the conditional entropy.
   3. the third line uses the fact the distortion for flipping the bit is infinite and hence for finite distortion given $Y=0$ or $Y=1$, $X$ is uniquely determined.
   4. the fourth line uses the fact that $X$ is binary and hence $H(X|Y=e)\le 1$.
   5. the last inequality is due to the fact that $P(Y=e)=Ed(X,Y)$ here (since the distortion is $1$ whenever $Y=e$ and otherwise it must be $0$ (same logic as point 3)). Thus, $P(Y=e)=Ed(X,Y)\le D$.

   Can we find a joint distribution in the feasible set that will satisfy the two inequalities with equality? The following construction does the job: let $B\sim Ber(D)$ be independent of $X$, and let $Y$ be given by $Y=e$ if $B=1$ and $Y=X$ otherwise. More explicitly, we set $P(X=0,Y=e)=P(X=1,Y=e)=\frac{D}{2}$ and $P(X=0,Y=0)=P(X=1,Y=1)=\frac{1-D}{2}$. The symmetry makes sure that $H(X|Y=e)=1$, and the choice of probabilities makes sure that $P(Y=e)=Ed(X,Y)=D$.

   b. [5 points] Suggest a simple and efficient scheme for some finite block size $k$ which achieves the optimal rate-distortion performance for this setting. You can assume that $D$ is rational, and may choose an appropriate value of $k$ accordingly.

   Hint: You can start working with a simple example where $D=\frac{1}{2},k=2$ and the optimal rate is $\frac{1}{2}$, i.e. you encode two input bits into a single codeword bit.

   Solution Since $D$ is rational, we can find block length $k$ such that $Dk$ and $(1-D)k$ are integers. The scheme to achieve optimal rate-distortion performance is quite simple: the encoder transmits the first $(1-D)k$ bits (hence the rate is $1-D$ bits/input symbol). The decoder fills the remaining $Dk$ positions with erasure $e$, hence achieving distortion of $D$.

Q2: Vector Quantization (20 points)

We have studied vector quantization (VQ) in class. In this question we will first implement part of vector quantization and then study the performance of vector quantization for a correlated gaussian process.

1. [10 points] Implement the build_kmeans_codebook() method in vector_quantizer.py. You cannot use the existing kmeans implementations for this part (e.g. build_kmeans_codebook_scipy() method) and must implement your own version. You can use the methods pre-implemented in vector_quantizer module. It will be instructive to look at the provided test cases in the module. Ensure that the test case test_vector_quantization passes on the provided data. You can use the following command to run the test cases:

   py.test -s -v vector_quantizer.py -k test_vector_quantization               
   

   Solution

   def build_kmeans_codebook(
           data_npy, num_vectors, dim, max_iter=100
   ):
       """
       data_npy -> [N] sized numpy array, where N is input data
       num_vectors -> number of vectors to add
       dim -> dimension in which to add the vectors
       max_iter -> the maximum number of iterations to run K-means for
       (you may terminate early if the vectors converge)
   
       output codebook -> [num_vectors,dim] numpy array
   
       Also, the expected output should be similar to build_kmeans_codebook_scipy
       (might not be exact same, due to initialization randomness)
       """
   
       #####################################################
       # ADD DETAILS HERE
       ######################################################
       # NOTE: initializing codebook to zeros as a placeholder
       # (added here to inform the expected return shape)
       codebook = np.zeros((num_vectors, dim))
       data_npy_2d = np.reshape(data_npy, [-1, dim])
   
       # TODO: add code here to set the codebook appropriately
       # using K-means. 
       # NOTE: don't directly call scipy/numpy library func 
       # which directly gives out K-means (duh)
       # NOTE: You may use mse(v1, v2), and find_nearest(codebook_npy, data_vector_npy, dist_func)
       # functions
       data_npy_2d = np.reshape(data_npy, [-1, dim])
   
       # TODO: add code here to set the codebook appropriately
       # using K-means
   
       # get random codebook
       codebook_start_indices = np.random.choice(data_npy_2d.shape[0], size=num_vectors, replace=False)
       for i in range(len(codebook_start_indices)):
           codebook[i, :] = data_npy_2d[codebook_start_indices[i], :]
   
       # do iterations
       for i in range(max_iter):
           vecs_in_codebook = {j: [] for j in range(num_vectors)}
           for k in range(data_npy_2d.shape[0]):
               distances = [mse(codebook[j, :], data_npy_2d[k, :]) for j in range(num_vectors)]
               nearest_codeword = distances.index(min(distances))
               vecs_in_codebook[nearest_codeword].append(data_npy_2d[k, :])
   
           # recompute mean
           for j in range(num_vectors):
               if len(vecs_in_codebook[j]) == 0:
                   continue
               else:
                   cumul = np.zeros((1, dim))
                   for v in vecs_in_codebook[j]:
                       cumul += v / len(vecs_in_codebook[j])
                   codebook[j, :] = cumul
   
       #####################################################
       return codebook
   

2. [10 points] Now we use the VQ to encode a correlated source. Consider a simple gaussian process where $$X_n=\rho X_{n-1}+\sqrt{1-{\rho }^2}\mathcal{N}(0,{\sigma }^2)$$ the second term is independent of $X_0,\dots ,X_{n-1}$, and $$X_0\sim \mathcal{N}(0,{\sigma }^2)$$

   Below we visualize the Rate-Distortion performance as well as encoding complexity for different values of $k$ (block sizes) and $\rho$ (parameter in the gaussian process), for a given rate of 1 bits per symbol. Based on these plots and what we have learnt in the class, answer following questions: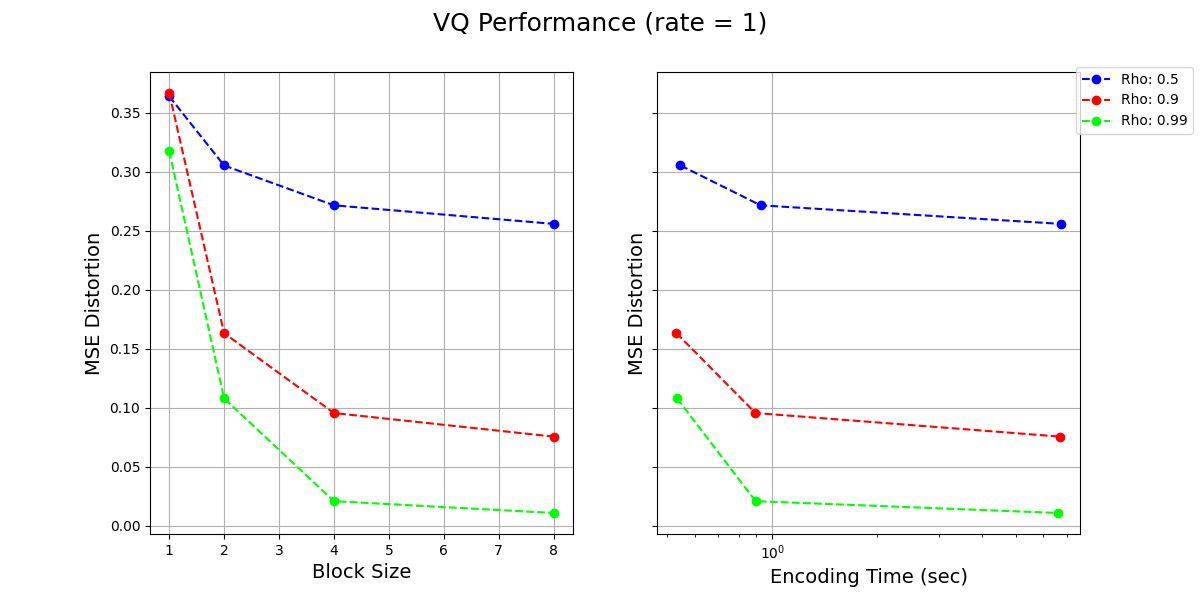

   

   How to read the plots? We fix rate = 1 and use vector quantization. The left plot shows the MSE distortion (y-axis) vs. the block size $k$ (x-axis) for different values of $\rho$. The right plot shows the MSE distortion (y-axis) vs. the Encoding Time (x-axis) for different values of $\rho$. Note that the points in the second plot correspond to different block sizes which can be inferred based on the matching MSE values from the first plot.

   a. [2 points] What is the theoretical distortion limit for $\rho =0$ at rate of 1 bits per symbol?

   Solution $\rho =0$ simplifies $X_n=\rho X_{n-1}+\sqrt{1-{\rho }^2}\mathcal{N}(0,{\sigma }^2)$ into $X_n=\mathcal{N}(0,{\sigma }^2)$. In class, we learned the rate-distortion function for a gaussian source with variance ${\sigma }^2$ is $$R(D)=\frac{1}{2}{\log }_2\frac{{\sigma }^2}{D}$$ When this rate is 1 bit per symbol, we have $$D=\frac{{\sigma }^2}{4}$$

   b. [4 points] What do you observe as $k$ increases for a given $\rho$? Comment on the performance and complexity of the encoder as $k$ increases. Justify your observations in a few lines.

   Solution As seen in the figure, as the block size, $k$, increases, the MSE distortion decreases for a given value of $\rho$. This is because vector quantization with higher $k$ can better exploit the dependence between the consecutive random variables, and also even for independent random variables at higher dimension we can better pack the space and get closer to the optimal rate distortion.

   As $k$ increases, we expect the time complexity of the encoder to increase as well because the number of codewords increases exponentially with $k$ and so does the time for encoding (which needs to search for the nearest codeword).

   c. [4 points] Focusing on the left plot, what do you observe as $\rho$ increases? Comment on how the change in performance of the encoder with increasing $k$ depends on the value of $\rho$. Justify your observations in a few lines.

   Solution As $\rho$ increases, the series becomes less random and more deterministic. At $\rho =1$, the series reduces to $X_n=X_{n-1}$. In this case, the MSE distortion is 0. This is because the series is completely deterministic and we can perfectly predict the next value in the series given the previous value.

   The bigger $\rho$ is, the bigger difference changing $k$ makes. This is because higher $k$ (block size) can capture the correlation and hence produce more benefit (as compared to the iid case where higher block size helps but only because of better codeword packing properties).

Q3: Lower Bounds via Information Theory (35 points)

At the annual Claude Shannon rowing contest, there are $n$ participants, with $n-1$ out of them having exactly same strength but one of the rowers is exceptionally strong. The contest aims at finding that one strongest rower. The competition organizers are unfortunately limited on the funds, and so want to minimize the number of rounds to declare the winner.

As a world renowned information theorist and compression expert, you have been roped in as a consultant, and have been tasked with deciding the match fixtures so that the exceptionally strong rower can be figured out in minimal number of matches. You have the following information:

• The matches can be between any two teams, where both team consists of an equal number of rowers. E.g. you can decide to have match between Rower 1 and Rower 2, or between (Rower 1, Rower 5) and (Rower 3, Rower 4) or between (Rower 1, Rower 4, Rower 5) and (Rower 2, Rower 3, Rower 6), etc.
• Each match can result in 3 outcomes: either the first team wins, or the second team wins, or it results in a draw. The team with the exceptionally strong rower always wins the match. If both the teams don't contain the strong rower, then the result is always a draw. Thus, the outcome of a fixture is deterministic given the team composition.
• Note that you are allowed to decide the teams in the second match based on the outcome of the first match, i.e. your match-deciding scheme can be adaptive.
• The teams in the matches should be chosen deterministically. They can depend on the outcome of previous matches, but not on any other random variable (e.g., you can't toss a coin to choose the teams!).

1. [10 points] Let the number of players be $n=9$. Show that you can determine the strongest rower using just 2 matches.

   Solution Split the 9 rowers into 3 groups of 3 rowers each. Let's call them $A$, $B$ and $C$. The following protocol finds the strongest rower in only two matches: Match 1: $A$ vs $B$. - If $A$ wins, then we know that the strongest rower is in $A$. Match 2: Choose two rowers from $A$ and match them against each other. If the match is a draw, then the third rower is the strongest rower. If one of the rowers wins, then that rower is the strongest rower. Without loss of generality, the same works if $B$ wins the first match. - If the result of Match 1 is a draw, then $C$ contains the strongest rower. Match 2 can be between any two rowers from $C$, and the result is the same as above.

2. [5 points] Generalize your strategy to $n$ rowers. Show that you can find one strongest rower in $\lceil {\log }_{3}n\rceil$ matches.

   Solution The above strategy can be generalized to $n$ rowers. We can split the $n$ rowers into 3 equal groups of size $\lfloor n/3\rfloor$ (if $n$ is not divisible by 3, then we set the remaining one or two rowers aside). Then, we implement the above strategy of pitting two of these groups against each other. If the result is a draw, then the third group contains the strongest rower. If one of the groups wins, then it contains the strongest rower. We can recursively apply the same strategy to the winning group. This strategy can be implemented in $\lceil {\log }_{3}n\rceil$ matches (since we reduce the set of candidates by a factor of $3$ at every step). If the strongest rower is in the remainder we set aside, then at worst, we need $O(1)$ additional matchs to determine the strongest rower. For large $n$, this is still in $\lceil {\log }_{3}n\rceil$.

To get your full fees, you have also been asked to prove that your strategy is indeed the optimal. Let $X$ be the random variable representing which player is the stronger rower. $X$ is uniformly distributed in the set of all participants $\{1,2,\dots ,n\}$ $$P_X(x=i)=\frac{1}{n},\forall i=\{1,2,\dots ,n\}$$

Let $Y_1,Y_2,\dots ,Y_k$ be the random variable representing the outcome of the $k$ matches you organize.

3. [5 points] Answer the following sub-problems.

   • Show that $H(X)={\log }_{2}n$, and $H(Y_i)\le lo{g}_{2}3$ for each $i$. When is equality achieved?
   • Explain why $H(Y_1,Y_2,\dots ,Y_k|X)=0$.

   Solution

   • $H(X)={\log }_{2}n$ because $X$ is uniformly distributed over $n$ elements. $Y_i$ can take on 3 values. To see this consider the $i^{th}$ match between two teams, which we will call the Cardinal and the Bears. $Y_i$ has three outcomes, 1. The Cardinal wins, 2. The Bears win, 3. The match is a draw. The entropy of $Y_i$ is maximized when the probability of each outcome is equal, so $H(Y_i)\le {\log }_{2}3$ where equality is achieved if the cases 1, 2, and 3 are equally likely.
   • $H(Y_1,Y_2,\dots ,Y_k|X)=0$ because the outcome of each match is deterministic given the strongest rower. If we know the strongest rower, then we know the outcome of each match. So, given the strongest rower, $X$, there is no uncertainty in the outcomes of the matches.

4. [10 points] We want to show that we will at least need ${\log }_{3}n$ matches to determine the strongest rower.

   • Show that we can determine the strongest rower from $k$ matches, if and only if $H(X|Y_1,Y_2,\dots ,Y_k)=0$.
   • Using the sub-problem above, show that $k\ge {\log }_{3}n$ matches are required to determine the strongest rower. Thus, proving that the scheme in Q4.1 is indeed optimal! (HINT: think about using $I(X;Y_1,\dots ,Y_k)$, and its properties).

   Solution

   • If $H(X|Y_1,Y_2,\dots ,Y_k)=0$, then $X$ is completely determined given $Y_1,Y_2,\dots ,Y_k$. This means that we can determine the strongest rower from $k$ matches. For the inverse direction, if we can determine the strongest rower from $k$ matches, then $X$ is completely determined given $Y_1,Y_2,\dots ,Y_k$. This means that $H(X|Y_1,Y_2,\dots ,Y_k)=0$.
   • The mutual information is: $$I\left(X;Y_1,\dots ,Y_k\right)=H(X)-H\left(X\mid Y_1,Y_2,\dots Y_k\right)=H\left(Y_1,Y_2,\dots Y_k\right)-H\left(Y_1,Y_2,\dots Y_k\mid X\right)$$

   We know that $H(Y_1,Y_2,\dots ,Y_k\mid X)=0$, so we can re-order the above equality to get: $$H(X)=H(Y_1,Y_2,\dots Y_k)+H\left(X\mid Y_1,Y_2,\dots Y_k\right)$$

   As shown in the previous sub-problem, we can only find the strongest rower from $k$ matches if $H\left(X\mid Y_1,Y_2,\dots Y_k\right)=0$, so any winning strategy will have:

   $$H(X)=H(Y_1,Y_2,\dots Y_k)$$ From part 3 above, we know that $H(X)={\log }_{2}n$ and $H(Y_i)\le {\log }_{2}3$ for all $i$, so we have $H(Y_1,Y_2,\dots Y_k)\le k{\log }_{2}3$. Yielding,

   $${\log }_{2}n\le k{\log }_{2}3$$

   So, $$k\ge \frac{{\log }_{2}n}{{\log }_{2}3}={\log }_{3}n$$

   Therefore, at least ${\log }_{3}n$ matches are required to determine the strongest rower.

5. [5 points] Let's get back to the $n=9$ rowers scenario. To simplify the logistics, the organizers wanted to pre-decide what the matches are going to be, even before the contest began. That is, the teams for the $i$ th match are pre-decided, and do not depend upon the outcome of the first $i-1$ matches. In other words the match deciding strategy is non-adaptive. Show that even in this non-adaptive case, you can find the strongest rower using the outcome of 2 pre-decided matches!

   Solution For the first round, we split the 9 rowers into 3 groups of 3 rowers each. Then, in the second round, we create 3 new groupings of 3 where no rower has a teammate that they had in the first round. For example, labeling the rowers 1 through 9, one possible arraingement could be:

   • Round 1: (1,2,3), (4,5,6), (7,8,9)
   • Round 2: (1,4,7), (2,5,8), (3,6,9)

   Ahead of time, we can randomly select two teams from this grouping to race each other in each round (e.g., we could do (1,2,3) vs. (4,5,6) and (1,4,7) vs. (3,6,9)). If a team wins a round, we know it contains the strongest rower, or in the case of a tie, we know that the third team contains the strongest rower. Since the teams consist of unique rowers the team we identify from Round 1 as containing the strongest rower will only have one rower in common with the team we identify from the second round as containing the strongest rower, allowing us to uniquely identify their identity!

Q4: Image Compression (40 points)

This question is about image compression. We will implement the transform coding ideas and use it to build a simple image compression scheme. Here are the instructions for this question:

• We have provided the code for this question both in the SCL HW repo as EE274_HW4_ImageCompressor.ipynb as well as a Google Colab notebook.
• We have tested the code on the Colab notebook, and we recommend working on the Colab notebook for this question. You should make a copy of the Colab notebook and work on the copy.
• The question has both coding and written parts. The written parts should be answered in the Colab notebook itself. You will need to run this notebook on Google Colab to answer some of the written parts.
• After working on the Colab notebook, you should download the notebook as a .ipynb file and submit it on Gradescope by replacing the existing EE274_HW4_ImageCompressor.ipynb file. This will be graded manually.

Solution Solution Notebook

Q5: HW4 Feedback (5 points)

Please answer the following questions, so that we can adjust the difficulty/nature of the problems for the next HWs.

1. How much time did you spent on the HW in total?
2. Which question(s) did you enjoy the most?
3. Are the programming components in the HWs helping you understand the concepts better?
4. Did the HW4 questions complement the lectures?
5. Any other comments?